📝题目描述#

给你个字符串，用其中所含数字组成一个最大的数字（每个数字只能用一次），输出这个最大的数字

比如说给你一个字符串 290es1q0，你就输出 92100

🧠思路#

水题一道

1. 模拟：遍历字符串 s，将其中所有数字储存到一个整数数组中
2. 贪心：
   1. 宁可多用，不能少用：所有数字都要用上
   2. 高数位对大数码：将整数数组从大到小排序

最后从头到尾打印整数数组就行了

💻Code#

时间复杂度：$O(n)$

1
#include <bits/stdc++.h>
2
using namespace std;
3
using ll = long long;
4
const int N = 1e6 + 7;
5

6
char s[N];
7
int a[N];
8

9
bool cmp(int x, int y){return x > y;}
10

11
int main()
12
{
13
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
14

15
    int ptr = 0;
16
    cin >> s;
17

18
    for(int i=0; i<int(strlen(s)); i++)
19
        if(s[i] >= '0' && s[i] <= '9')
20
            a[ptr ++] = s[i] - '0';
21

22
    sort(a, a+ptr, cmp);
23

24
    for(int i=0; i<ptr; i++) cout << a[i];
25
}

📝题目描述#

给你一个整数数组和两个整数 n 和 m

将该数组中所有数字从大到小蛇形地排入一个 n*m 的矩形中（数组中的数各不相同），如图：

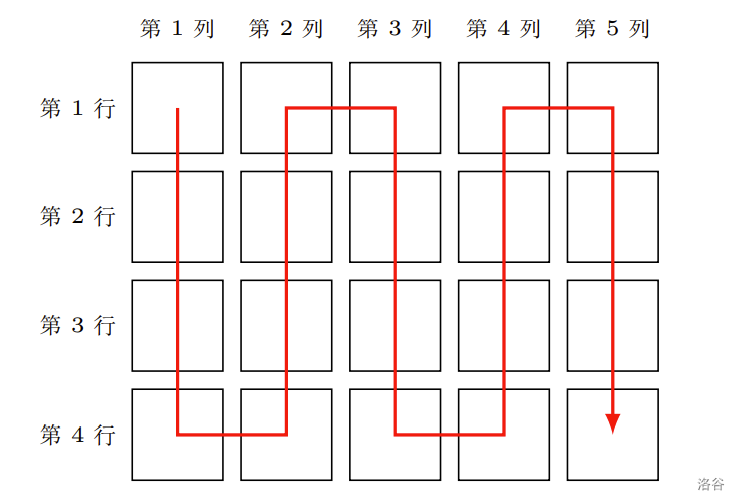
输出该整数数组的第一个数在矩形中的位置（即输出第几列，第几行）

🧠思路#

数学题一枚

我们先统计出有多少个数大于整数数组的第一个数，记作 p

则这个 p 就相当于“座位号”

再记 p 在蛇形矩阵中对应第 c 列，第 r 行

观察图片，就有：

• 当 c 为奇数时，r 随 p 的增大而增大

• 当 c 为偶数时，r 随 p 的增大而减小

运用一下小学数学：

1. 直接算出：$c = \displaystyle \lceil{\frac p n}\rceil = \frac {p-1} n +1$（这里使用了 C++ 除法自动向下取整的特性）

2. 根据 c 的奇偶性算出 r，记得考虑 p%n = 0 的情况：

   • 当 p%n = 0 且 c 为奇数时，r = n
   • 当 p%n = 0 且 c 为偶数时，r = 1
   • 当 p%n ≥ 1 且 c 为奇数时，r = p%n
   • 当 p%n ≥ 1 且 c 为偶数时，r = n-(p%n)+1

最后依次输出 c 和 r

💻Code#

时间复杂度：$O(nm)$

1
#include <bits/stdc++.h>
2
using namespace std;
3
using ll = long long;
4
const int N = 1e5 + 7;
5

6
int a[N];
7

8
int main()
9
{
10
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
11

12
    int n, m; cin >> n >> m;
13
    for(int i=1; i<=n*m; i++) cin >> a[i];
14

15
    int p = 1;
16
    for(int i=2; i<=n*m; i++) p += (a[i] > a[1]);
17

18
    int c = (p-1)/n + 1, r;
19
    if(c&1)
20
        if(p%n) r = p%n;
21
        else r = n;
22
    else
23
        if(p%n) r = n-(p%n)+1;
24
        else r = 1;
25

26
    cout << c << ' ' << r;
27
}

📝题目描述#

给你一个长度为 n 的非负整数数组 a 和一个非负整数 k

请选择数组 a 中尽可能多的不相交的区间，使得区间内每个整数的二进制按位异或和（即$\oplus$）等于 k

输出你能最多能在 a 选出多少个这样的区间

🧠思路#

这才是 CSP-J 应有的难度！

首先由区间联想到前缀和，我们可以用类似前缀和的方式快速求区间异或和

这里记前缀异或和数组为 p，则当 $p_l\oplus p_r = k$ 时：$[a_{l+1},a_r]$ 是一个符合条件的区间

接着根据异或性质进行转化：

再定义上一个区间的右端点位置为 lst，用于判断区间是否重叠

于是，我们就可以通过枚举右端点 r，并寻找左端点 l 的方式来寻找合法区间

且每次找到合法区间后执行 lst = r，这个 lst 是需要我们维护的

那么如何寻找左端点 l 呢？有人想用枚举（会超时），这里我们用哈希表

对于 p 中的每个数据，我们将其值作为下标，位置作为值去维护一个哈希表

这样访问时只需将 $p_r\oplus k$ 作为下标传进这个哈希表，便能得到一个位置，这个位置就是待定的左端点

IMPORTANT

由于在每次遍历时，维护哈希值的代码都会被执行，这就导致了哈希表中某下标所对的值是可变的

具体地，对于 p 中两个相同的数据，哈希表会记录 p 中更靠后的数据的位置，并覆盖掉原先记录的位置

这会有什么影响吗？

首先，这点微小的变化无非涉及到两个位置，我们分别记作位置 x、y（其中 x < y）

假设现在 x < lst < y，则我们已经用 y 覆盖了 x，故左端点 y 有效，与当前右端点 r 构成一个有效区间

但如果没有上述机制，则哈希表记录的是位置 x，故左端点 x 无效，不能与当前右端点 r 构成一个有效区间

此处这个小细节就是运用了贪心算法，它在暗地里帮我们增加了有效区间的个数

当然在此之前我们已经不知不觉地用上了贪心算法…

什么？我们啥时候贪的？

很简单：当初我们优先选择最早结束的合法区间，这样就有 $lst = r_{min}$，从而为后续预留更多选择空间

由于这里的贪心不需要我们刻意实现：在从头至尾地遍历 p 时，只要每发现一个合法右端点就去记录这个区间，就自然而然地运用上了

故有很多人在没有意识到的情况下就把题过了，属实可惜！

最后，在双贪心和前缀和的思想下，代码呼之欲出

💻Code#

时间复杂度：$O(n)$

1
#include <bits/stdc++.h>
2
using namespace std;
3
using ll = long long;
4
const int N = 5e6 + 7;
5

6
ll a[N], pre[N];
7
int hsh[N];
8

9
int main()
10
{
11
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
12

13
    int n, k; cin >> n >> k;
14
    for(int i=1; i<=n; i++) cin >> a[i];
15

16
    for(int i=1; i<=n; i++) pre[i] = pre[i-1] ^ a[i];
17

18
    ll lst = 0, ans = 0;
19

20
    memset(hsh,-1,sizeof hsh);
21
    hsh[0] = 0;
22

23
    for(int i=1; i<=n; i++)
24
    {
25
        ll x = pre[i] ^ k;
26
        if(hsh[x] >= lst)
27
        {
28
            ans ++;
29
            lst = i;
30
        }
31
        hsh[pre[i]] = i;
32
    }
33

34
    cout << ans;
35
    return 0;
36
}